Welcome to our Support Center
Updated

MeanVarianceNormalization

Description

A MeanVarianceNormalization Function: Perform mean variance normalization on the input tensor X using formula: (X-EX)/sqrt(E(X-EX)^2)

 

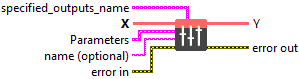
Input parameters

 

specified_outputs_name : array, this parameter lets you manually assign custom names to the output tensors of a node.
 X (heterogeneous) – T : object, input tensor.

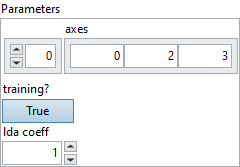
 Parameters : cluster,

axes : array, a list of integers, along which to reduce. The default is to calculate along axes [0,2,3] for calculating mean and variance along each channel. Two variables with the same C-coordinate are associated with the same mean and variance.
Default value “[0, 2, 3]”.
 training? : boolean, whether the layer is in training mode (can store data for backward).
Default value “True”.
 lda coeff : float, defines the coefficient by which the loss derivative will be multiplied before being sent to the previous layer (since during the backward run we go backwards).
Default value “1”.

 name (optional) : string, name of the node.

Output parameters

 

 Y (heterogeneous) – T : object, output tensor.

Type Constraints

T in (tensor(bfloat16), tensor(double), tensor(float), tensor(float16)) : Constrain input and output types to all numeric tensors.

Example

All these exemples are snippets PNG, you can drop these Snippet onto the block diagram and get the depicted code added to your VI (Do not forget to install Deep Learning library to run it).
Table of Contents