-
Quick start
-
API
-
-
- Resume
- Add
- AdditiveAttention
- AlphaDropout
- Attention
- Average
- AvgPool1D
- AvgPool2D
- AvgPool3D
- BatchNormalization
- Bidirectional
- Concatenate
- Conv1D
- Conv1DTranspose
- Conv2D
- Conv2DTranspose
- Conv3D
- Conv3DTranspose
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Cropping1D
- Cropping2D
- Cropping3D
- Dense
- DepthwiseConv2D
- Dropout
- ELU
- Embedding
- Exponential
- Flatten
- GaussianDropout
- GaussianNoise
- GELU
- GlobalAvgPool1D
- GlobalAvgPool2D
- GlobalAvgPool3D
- GlobalMaxPool1D
- GlobalMaxPool2D
- GlobalMaxPool3D
- GRU
- HardSigmoid
- Input
- LayerNormalization
- LeakyReLU
- Linear
- LSTM
- MaxPool1D
- MaxPool2D
- MaxPool3D
- MultiHeadAttention
- Multiply
- Output Predict
- Output Train
- Permute3D
- PReLU
- ReLU
- Reshape
- RNN
- SELU
- SeparableConv1D
- SeparableConv2D
- Sigmoid
- SimpleRNN
- SoftMax
- SoftPlus
- SoftSign
- SpatialDropout
- Split
- Substract
- Swish
- TanH
- ThresholdedReLU
- UpSampling1D
- UpSampling2D
- UpSampling3D
- ZeroPadding1D
- ZeroPadding2D
- ZeroPadding3D
- Show All Articles (64) Collapse Articles
-
-
-
-
- Abs
- Acos
- Acosh
- ArgMax
- ArgMin
- Asin
- Asinh
- Atan
- Atanh
- AveragePool
- Bernouilli
- BitwiseNot
- BlackmanWindow
- Cast
- Ceil
- Celu
- ConcatFromSequence
- Cos
- Cosh
- DepthToSpace
- Det
- DynamicTimeWarping
- Erf
- Exp
- EyeLike
- Flatten
- Floor
- GlobalAveragePool
- GlobalLpPool
- GlobalMaxPool
- HammingWindow
- HannWindow
- HardSwish
- HardMax
- Identity
- ImageDecoder
- Inverse
- lrfft
- lslnf
- lsNaN
- Log
- LogSoftmax
- LpNormalization
- LpPool
- LRN
- MeanVarianceNormalization
- MicrosoftGelu
- Mish
- Multinomial
- MurmurHash3
- Neg
- NhwcMaxPool
- NonZero
- Not
- OptionalGetElement
- OptionalHasElement
- QuickGelu
- RandomNormalLike
- RandomUniformLike
- RawConstantOfShape
- Reciprocal
- ReduceSumInteger
- RegexFullMatch
- Rfft
- Round
- SampleOp
- SequenceLength
- Shape
- Shrink
- Sign
- Sin
- Sinh
- Size
- SpaceToDepth
- Sqrt
- StringNormalizer
- Tan
- TfldfVectorizer
- Tokenizer
- Transpose
- UnfoldTensor
- Show All Articles (66) Collapse Articles
-
-
-
- Add
- AffineGrid
- And
- BiasAdd
- BiasGelu
- BiasSoftmax
- BiasSplitGelu
- BitShift
- BitwiseAnd
- BitwiseOr
- BitwiseXor
- CastLike
- CDist
- CenterCropPad
- Clip
- Col2lm
- ComplexMul
- ComplexMulConj
- Compress
- Conv
- ConvInteger
- ConvTranspose
- ConvTransposeWithDynamicPads
- CropAndResize
- CumSum
- DeformConv
- DequantizeBFP
- DequantizeLinear
- DequantizeWithOrder
- DFT
- Div
- DynamicQuantizeMatMul
- Equal
- Expand
- ExpandDims
- FastGelu
- FusedConv
- FusedGemm
- FusedMatMul
- FusedMatMulActivation
- GatedRelativePositionBias
- Gather
- GatherElements
- GatherND
- Gemm
- GemmFastGelu
- GemmFloat8
- Greater
- GreaterOrEqual
- GreedySearch
- GridSample
- GroupNorm
- InstanceNormalization
- Less
- LessOrEqual
- LongformerAttention
- MatMul
- MatMulBnb4
- MatMulFpQ4
- MatMulInteger
- MatMulInteger16
- MatMulIntergerToFloat
- MatMulNBits
- MaxPoolWithMask
- MaxRoiPool
- MaxUnPool
- MelWeightMatrix
- MicrosoftDequantizeLinear
- MicrosoftGatherND
- MicrosoftGridSample
- MicrosoftPad
- MicrosoftQLinearConv
- MicrosoftQuantizeLinear
- MicrosoftRange
- MicrosoftTrilu
- Mod
- MoE
- Mul
- MulInteger
- NegativeLogLikelihoodLoss
- NGramRepeatBlock
- NhwcConv
- NhwcFusedConv
- NonMaxSuppression
- OneHot
- Or
- PackedAttention
- PackedMultiHeadAttention
- Pad
- Pow
- QGemm
- QLinearAdd
- QLinearAveragePool
- QLinearConcat
- QLinearConv
- QLinearGlobalAveragePool
- QLinearLeakyRelu
- QLinearMatMul
- QLinearMul
- QLinearReduceMean
- QLinearSigmoid
- QLinearSoftmax
- QLinearWhere
- QMoE
- QOrderedAttention
- QOrderedGelu
- QOrderedLayerNormalization
- QOrderedLongformerAttention
- QOrderedMatMul
- QuantizeLinear
- QuantizeWithOrder
- Range
- ReduceL1
- ReduceL2
- ReduceLogSum
- ReduceLogSumExp
- ReduceMax
- ReduceMean
- ReduceMin
- ReduceProd
- ReduceSum
- ReduceSumSquare
- RelativePositionBias
- Reshape
- Resize
- RestorePadding
- ReverseSequence
- RoiAlign
- RotaryEmbedding
- ScatterElements
- ScatterND
- SequenceAt
- SequenceErase
- SequenceInsert
- Slice
- SparseToDenseMatMul
- SplitToSequence
- Squeeze
- STFT
- StringConcat
- Sub
- Tile
- TorchEmbedding
- TransposeMatMul
- Trilu
- Unsqueeze
- Where
- WordConvEmbedding
- Xor
- Show All Articles (134) Collapse Articles
-
- Attention
- AttnLSTM
- BatchNormalization
- BiasDropout
- BifurcationDetector
- BitmaskBiasDropout
- BitmaskDropout
- DecoderAttention
- DecoderMaskedMultiHeadAttention
- DecoderMaskedSelfAttention
- Dropout
- DynamicQuantizeLSTM
- EmbedLayerNormalization
- GemmaRotaryEmbedding
- GroupQueryAttention
- GRU
- LayerNormalization
- LSTM
- MicrosoftMultiHeadAttention
- QAttention
- RemovePadding
- RNN
- Sampling
- SkipGroupNorm
- SkipLayerNormalization
- SkipSimplifiedLayerNormalization
- SoftmaxCrossEntropyLoss
- SparseAttention
- TopK
- WhisperBeamSearch
- Show All Articles (15) Collapse Articles
-
-
-
-
-
-
- Resume
- Constant
- GlorotNormal
- GlorotUniform
- HeNormal
- HeUniform
- Identity
- LecunNormal
- LecunUniform
- Ones
- Orthogonal
- RandomNormal
- RandomUnifom
- TruncatedNormal
- VarianceScaling
- Zeros
- Show All Articles (1) Collapse Articles
-
- Resume
- BinaryCrossentropy
- CategoricalCrossentropy
- CategoricalHinge
- CosineSimilarity
- Hinge
- Huber
- KLDivergence
- LogCosh
- MeanAbsoluteError
- MeanAbsolutePercentageError
- MeanSquaredError
- MeanSquaredLogarithmicError
- Poisson
- SquaredHinge
- Custom
- Show All Articles (1) Collapse Articles
-
-
-
-
-
- Dense
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- AdditiveAttention
- Attention
- MutiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- Embedding
- BatchNormalization
- LayerNormalization
- Bidirectional
- GRU
- LSTM
- SimpleRNN
- Show All Articles (12) Collapse Articles
-
- Dense
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- Embedding
- BatchNormalization
- LayerNormalization
- Bidirectional
- GRU
- LSTM
- SimpleRNN
- Show All Articles (12) Collapse Articles
-
-
- Resume
- Dense
- AdditiveAttention
- Attention
- MultiHeadAttention
- BatchNormalization
- LayerNormalization
- Bidirectional
- GRU
- LSTM
- SimpleRNN
- Conv1D
- Conv2D
- Conv3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- Embedding
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Show All Articles (13) Collapse Articles
-
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- Show All Articles (15) Collapse Articles
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- Show All Articles (15) Collapse Articles
-
-
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- Show All Articles (15) Collapse Articles
-
- Dense
- Embedding
- AdditiveAttention
- Attention
- MultiHeadAttention
- Conv1D
- Conv2D
- Conv3D
- ConvLSTM1D
- ConvLSTM2D
- ConvLSTM3D
- Conv1DTranspose
- Conv2DTranspose
- Conv3DTranspose
- DepthwiseConv2D
- SeparableConv1D
- SeparableConv2D
- BatchNormalization
- LayerNormalization
- PReLU 2D
- PReLU 3D
- PReLU 4D
- PReLU 5D
- Bidirectional
- GRU
- LSTM
- RNN (GRU)
- RNN (LSTM)
- RNN (SimpleRNN)
- SimpleRNN
- Show All Articles (15) Collapse Articles
-
-
- Resume
- Accuracy
- BinaryAccuracy
- BinaryCrossentropy
- BinaryIoU
- CategoricalAccuracy
- CategoricalCrossentropy
- CategoricalHinge
- CosineSimilarity
- FalseNegatives
- FalsePositives
- Hinge
- Huber
- IoU
- KLDivergence
- LogCoshError
- Mean
- MeanAbsoluteError
- MeanAbsolutePercentageError
- MeanIoU
- MeanRelativeError
- MeanSquaredError
- MeanSquaredLogarithmicError
- MeanTensor
- OneHotIoU
- OneHotMeanIoU
- Poisson
- Precision
- PrecisionAtRecall
- Recall
- RecallAtPrecision
- RootMeanSquaredError
- SensitivityAtSpecificity
- SparseCategoricalAccuracy
- SparseCategoricalCrossentropy
- SparseTopKCategoricalAccuracy
- Specificity
- SpecificityAtSensitivity
- SquaredHinge
- Sum
- TopKCategoricalAccuracy
- TrueNegatives
- TruePositives
- Show All Articles (28) Collapse Articles
-
-
GatherND
Description
Given data tensor of rank r >= 1, indices tensor of rank q >= 1, and batch_dims integer b, this operator gathers slices of data into an output tensor of rank q + r - indices_shape[-1] - 1 - b.
indices is an q-dimensional integer tensor, best thought of as a (q-1)-dimensional tensor of index-tuples into data, where each element defines a slice of data
batch_dims (denoted as b) is an integer indicating the number of batch dimensions, i.e the leading b number of dimensions of data tensor and indices are representing the batches, and the gather starts from the b+1 dimension.
Some salient points about the inputs’ rank and shape:
- r >= 1 and q >= 1 are to be honored. There is no dependency condition to be met between ranks
randq - The first
bdimensions of the shape ofindicestensor anddatatensor must be equal. - b < min(q, r) is to be honored.
- The
indices_shape[-1]should have a value between 1 (inclusive) and rankr-b(inclusive) - All values in
indicesare expected to be within bounds [-s, s-1] along axis of sizes(i.e.)-data_shape[i] <= indices[...,i] <= data_shape[i] - 1. It is an error if any of the index values are out of bounds.
The output is computed as follows:
The output tensor is obtained by mapping each index-tuple in the indices tensor to the corresponding slice of the input data.
- If
indices_shape[-1] > r-b=> error condition - If
indices_shape[-1] == r-b, since the rank ofindicesisq,indicescan be thought of asN(q-b-1)-dimensional tensors containing 1-D tensors of dimensionr-b, whereNis an integer equals to the product of 1 and all the elements in the batch dimensions of the indices_shape. Let us think of each suchr-branked tensor asindices_slice. Each scalar value corresponding todata[0:b-1,indices_slice]is filled into the corresponding location of the(q-b-1)-dimensional tensor to form theoutputtensor (Example 1 below) - If
indices_shape[-1] < r-b, since the rank ofindicesisq,indicescan be thought of asN(q-b-1)-dimensional tensor containing 1-D tensors of dimension< r-b. Let us think of each such tensors asindices_slice. Each tensor slice corresponding todata[0:b-1, indices_slice , :]is filled into the corresponding location of the(q-b-1)-dimensional tensor to form theoutputtensor (Examples 2, 3, 4 and 5 below)
This operator is the inverse of ScatterND.
Input parameters
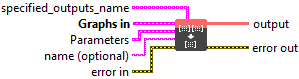
![]() specified_outputs_name : array, this parameter lets you manually assign custom names to the output tensors of a node.
specified_outputs_name : array, this parameter lets you manually assign custom names to the output tensors of a node.
![]() Graphs in : cluster, ONNX model architecture.
Graphs in : cluster, ONNX model architecture.
![]() data (heterogeneous) – T : object, tensor of rank r >= 1.
data (heterogeneous) – T : object, tensor of rank r >= 1.![]() indices (heterogeneous) – tensor(int64) : object, tensor of rank q >= 1. All index values are expected to be within bounds [-s, s-1] along axis of size s. It is an error if any of the index values are out of bounds.
indices (heterogeneous) – tensor(int64) : object, tensor of rank q >= 1. All index values are expected to be within bounds [-s, s-1] along axis of size s. It is an error if any of the index values are out of bounds.

![]() Parameters : cluster,
Parameters : cluster,
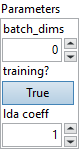
![]() batch_dims : integer, the number of batch dimensions. The gather of indexing starts from dimension of data[batch_dims:].
batch_dims : integer, the number of batch dimensions. The gather of indexing starts from dimension of data[batch_dims:].
Default value “0”.![]() training? : boolean, whether the layer is in training mode (can store data for backward).
training? : boolean, whether the layer is in training mode (can store data for backward).
Default value “True”.![]() lda coeff : float, defines the coefficient by which the loss derivative will be multiplied before being sent to the previous layer (since during the backward run we go backwards).
lda coeff : float, defines the coefficient by which the loss derivative will be multiplied before being sent to the previous layer (since during the backward run we go backwards).
Default value “1”.
![]() name (optional) : string, name of the node.
name (optional) : string, name of the node.
Output parameters
![]() output (heterogeneous) – T : object, tensor of rank q + r – indices_shape[-1] – 1.
output (heterogeneous) – T : object, tensor of rank q + r – indices_shape[-1] – 1.
Type Constraints
T in (tensor(bfloat16), tensor(bool), tensor(complex128), tensor(complex64), tensor(double), tensor(float), tensor(float16), tensor(int16), tensor(int32), tensor(int64), tensor(int8), tensor(string), tensor(uint16), tensor(uint32), tensor(uint64), tensor(uint8)) : Constrain input and output types to any tensor type.

